C. Primes or Palindromes?

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Rikhail Mubinchik believes that the current definition of prime numbers is obsolete as they are too complex and unpredictable. A palindromic number is another matter. It is aesthetically pleasing, and it has a number of remarkable properties. Help Rikhail to convince the scientific community in this!
Let us remind you that a number is called prime if it is integer larger than one, and is not divisible by any positive integer other than itself and one.
Rikhail calls a number a palindromic if it is integer, positive, and its decimal representation without leading zeros is a palindrome, i.e. reads the same from left to right and right to left.
One problem with prime numbers is that there are too many of them. Let's introduce the following notation: π(n) — the number of primes no larger than n, rub(n) — the number of palindromic numbers no larger than n. Rikhail wants to prove that there are a lot more primes than palindromic ones.
He asked you to solve the following problem: for a given value of the coefficient A find the maximum n, such that π(n) ≤ A·rub(n).

Input

The input consists of two positive integers p, q, the numerator and denominator of the fraction that is the value of A (, ).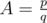

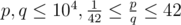Output

If such maximum number exists, then print it. Otherwise, print "Palindromic tree is better than splay tree" (without the quotes).

Sample test(s)

Input

1 1

Output

40

Input

1 42

Output

1

Input

6 4

Output

172

The key thing of this question was the calculation of the highest number till which n 

can go, and this is briefly expalined in the context editorials.

It is known that amount of prime numbers non greater than n is about .
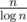We can also found the amount of palindrome numbers with fixed length k — it is about 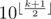which is .
Therefore the number of primes asymptotically bigger than the number of palindromic numbers and for every constant A there is an answer. Moreover, for this answer n the next condition hold: . In our case n < 10⁷.
For all numbers smaller than 10⁷ we can check if they are primes (via sieve of Eratosthenes) and/or palindromes (via trivial algorithm or compute reverse number via dynamic approach). Then we can calculate prefix sums (π(n) and rub(n)) and find the answer using linear search.
For A ≤ 42 answer is smaller than 2·10⁶.
Complexity — .


Now , it is easy to see that  we calculate the primes till 2*10^6 and palindromes upto that range and store them in an array. After this is done , we just check form manx to 0 to see if the condition is satisfied. If yes we take it as the maximum number.

******* Here goes the code*****

#include<bits/stdc++.h>
using namespace std;
int sv[2000010];
int n=1200000;
int palinhash[2000010];
char c[20];
int numpr[2000010];
            int      numprcnt[2000010];
            int palin[2000010];
            int palincnt[2000010];
int sumpr[2000100];
    int sumpalin[2000100];
    bool ispal(int x) {
  int l = 0;
  while(x>0) {
    c[l] = x%10;
    l++;
    x/=10;
  }
  for(int i=0; i<l/2; i++) {
    if(c[i]!=c[l-i-1]) return 0;
  }
  return 1;
}

void seive()

{
    //cout<<"started "<<endl;
    sv[2]=0;
    for(int i=2;i<=sqrt(n);i++)
    {
          if(!sv[i])
          {
             for(int j=2;j*i<=n;j++)
             {
                   sv[i*j]++;
               }
          }
    }
}
int main()
{
    int t;
    seive();
   // cout<<"dne "<<endl;
    int top=0;
   
//  cout<<"here "<<endl;
    int val=0;
    int last=0;
    for(int i=1;i<=n;i++)
    {
        
         // int l=strlen(str);
          if(ispal(i))
          {
                
                 palinhash[i]++;
               
          }
         
        
    }
  //cout<<n<<endl;
   
    int p;
    int q;
   
    sumpr[0]=0;
    sumpalin[0]=0;
    sv[1]=1;
      for(int i=1;i<=2000001;i++)
      {
        sumpalin[i]=sumpalin[i-1];
        sumpr[i]=sumpr[i-1];
         if(sv[i]==0)
         {
           
         // cout<<"hjere "<<i<<endl;
               sumpr[i]=1+sumpr[i-1];
           }
           if(palinhash[i]==1)
           {
         //     cout<<i<<" ";
              sumpalin[i]=1+sumpalin[i-1];
           }
      }
     
     
   //   cout<<sumpalin[10001]<<endl;
    // cout<<sumpr[100001]<<endl;
     cin>>p>>q;
   
     double a = (double)p / q;
      int ans=0;
  for (int i = n; i >0; i--) {
    if((double)sumpr[i] <= (double)a*sumpalin[i]){
    //  ans=i;
       cout<<i<<endl;
       return 0;
    }
  }
 

 
  cout << "Palindromic tree is better than splay tree" << std::endl;
  return 0;
}
********* ends      here* ***