A. Little Pony and Expected Maximum
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output
Twilight Sparkle was playing Ludo with her friends Rainbow Dash, Apple Jack and Flutter Shy. But she kept losing. Having returned to the castle, Twilight Sparkle became interested in the dice that were used in the game.
The dice has m faces: the first face of the dice contains a dot, the second one contains two dots, and so on, the m-th face contains mdots. Twilight Sparkle is sure that when the dice is tossed, each face appears with probability  . Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice n times.
. Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice n times.
 . Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice n times.
. Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice n times.
Input
A single line contains two integers m and n (1 ≤ m, n ≤ 105).
Output
Output a single real number corresponding to the expected maximum. The answer will be considered correct if its relative or absolute error doesn't exceed 10 - 4.
Sample test(s)
input
6 1
output
3.500000000000
input
6 3
output
4.958333333333
input
2 2
output
1.750000000000
Note
Consider the third test example. If you've made two tosses:
- You can get 1 in the first toss, and 2 in the second. Maximum equals to 2.
- You can get 1 in the first toss, and 1 in the second. Maximum equals to 1.
- You can get 2 in the first toss, and 1 in the second. Maximum equals to 2.
- You can get 2 in the first toss, and 2 in the second. Maximum equals to 2.
The probability of each outcome is 0.25, that is expectation equals to:

You can read about expectation using the following link: http://en.wikipedia.org/wiki/Expected_value
This is a question based on observation and the observation has to be kept on mind. First read the editorial
Brief description:
Calculate the expected maximum number after tossing a m faces dice n times.
Analysis:
Take m = 6, n = 2 as a instance.
6 6 6 6 6 6
5 5 5 5 5 6
4 4 4 4 5 6
3 3 3 4 5 6
2 2 3 4 5 6
1 2 3 4 5 6
Enumerate the maximum number, the distribution will be a n-dimensional super-cube with m-length-side. Each layer will be a large cube minus a smaller cube. So we have:
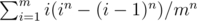
No comments:
Post a Comment