Fatal Eagle has decided to do something to save his favorite city against the attack of Mr. XYZ, since no one else surprisingly seems bothered about it, and are just suffering through various attacks by various different creatures.
Seeing Fatal Eagle's passion, N members of the Bangalore City decided to come forward to try their best in saving their city. Now Fatal Eagle decided to strategize these N people into a formation of AT LEAST K people in a group. Otherwise, that group won't survive.
Let's demonstrate this by an example. Let's say that there were 10 people, and each group required at least 3 people in it for its survival. Then, the following 5 groups can be made:
- 10 - Single group of 10 members.
- 7, 3 - Two groups. One consists of 7 members, the other one of 3 members.
- 6, 4 - Two groups. One consists of 6 members, the other one of 4 members.
- 5, 5 - Two groups. One consists of 5 members, the other one of 5 members.
- 4, 3, 3 - Three groups. One consists of 4 members, the other two of 3 members.
Given the value of N, and K - help Fatal Eagle in finding out the number of ways he can form these groups (anti-squads) to save his city.
Input format:
The first line would contain, T - denoting the number of test cases, followed by two integers, N and K denoting the number of people who're willing to help and size of the smallest possible group which can be formed.
The first line would contain, T - denoting the number of test cases, followed by two integers, N and K denoting the number of people who're willing to help and size of the smallest possible group which can be formed.
Output format:
You've to print the number of ways in which groups can be formed.
You've to print the number of ways in which groups can be formed.
Constraints:
1 <= T <= 30
1 <= N, K <= 200
1 <= T <= 30
1 <= N, K <= 200
Sample Input
(Plaintext Link)2 10 3 20 5
Sample Output
(Plaintext Link)5 13
A very good way to brush up recursive DPs. Here the given problem is a variation of the standard integer partition problem . Only the limitation being, the group size should be atleast k.To do these first we understand that how things are broken up. An important observation is for thinks like 7 and k=3 we may repeat the counting of the group like (4,3) and (3,4). So , I suggest recursuve manner.
No we keep two things in our recursion the left number of soldiers to be allotted and the last alloted group. We always try to ensure the fact that the present group is given more than equal to the last group and obviously greater than K. the base cases are
(1) If dp is known return it;
(2) If present falls to 0 return 1, becuase that arrangment is possible.
(3) If present is less than K than forming that group is impossible so return 0;
The code goes here
#include<bits/stdc++.h>
using namespace std;
long long int dp[250][250];
long long int solve(int present, int k,int prev )
{
//cout<<present<<" "<<prev<<endl;
if(present==0)
return 1;
if(present<k)
return 0;
if(dp[present][prev]!=-1)
return dp[present][prev];
else
{
dp[present][prev]=0;
for(int i=k;i<=present;i++)
{
if(i>=prev)
dp[present][prev]+=solve(present-i,k,i);
}
// cout<<"returning dp "<<present <<" "<<prev<<" "<<dp[present][prev]<< endl;
return dp[present][prev];
}
}
int main()
{
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
int k;
cin>>k;
for(int i=0;i<210;i++)
{
for(int j=0;j<210;j++)
dp[i][j]=-1;
}
long long int ans=solve(n,k,0);
cout<<ans<<endl;
}
return 0;
}
 . Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice
. Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice 
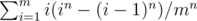

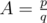 ,
, 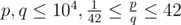 ).
).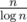 .
.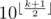 which is
which is  .
. . In our case
. In our case  .
.