Kitty and Katty have N$N$ plastic blocks. They label the blocks with sequential numbers from 1$1$to N$N$ and begin playing a game in turns, with Kitty always taking the first turn. The game's rules are as follows:

• For each turn, the player removes 2$2$ blocks, A$A$ and B$B$, from the set. They calculate A−B$A-B$, write the result on a new block, and insert the new block into the set.
• The game ends when only 1$1$ block is left. The winner is determined by the value written on the final block, X$X$:
  • If X%3=1$X\mathrm{\%}3=1$, then Kitty wins.
  • If X%3=2$X\mathrm{\%}3=2$, then Katty wins.
  • If X%3=0$X\mathrm{\%}3=0$, then the player who moved last wins.

Recall that %$\mathrm{\%}$ is the Modulo Operation.

Given the value of N$N$, can you find and print the name of the winner? Assume that both play optimally.

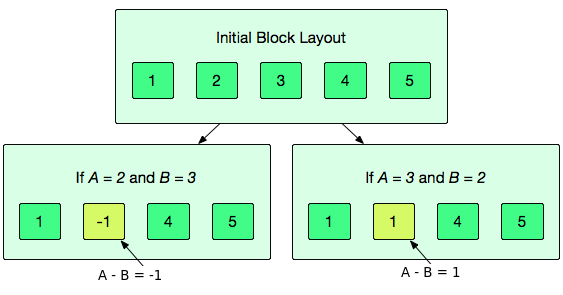
Note: The selection order for A$A$ and B$B$ matters, as sometimes A−B≠B−A$A-B\ne B-A$. The diagram below shows an initial set of blocks where N=5$N=5$. If A=2$A=2$ and B=3$B=3$, then the newly inserted block is labeled −1$-1$; alternatively, if A=3$A=3$ and B=2$B=2$, the newly inserted block is labeled 1$1$.

Input Format

The first line contains a single positive integer, T$T$ (the number of test cases or games). 
The T$T$ subsequent lines each contain an integer, N$N$ (the number of blocks for that test case).

Constraints

• 1≤T≤100$1\le T\le 100$
• 1≤N≤105$1\le N\le {10}^5$

Output Format

For each test case, print the name of the winner (i.e.: either Kitty or Katty) on a new line.

Editorial

Special Case

Let us first deal with the special case. When `N=1$N=1$`, there is only one element in the array, and nobody can make a move. Kitty wins since the remainder is `1$1$`.

Solution

For any arbitary `N>1$N>1$`, imagine the game is being played. Eventually, the game will come to a situation when there are exactly two elements in the array, `A$A$` and `B$B$`. Since the game is decided by the final value modulo `3$3$`, we can say that `a=A%3$a=A\mathrm{\%}3$` and `b=B%3$b=B\mathrm{\%}3$` and play with these two numbers instead. It will not affect the game state.

Now, if `a=b$a=b$`, then this player can simply replace `a,b$a,b$` with `a−b=0$a-b=0$`. The final value will be `0$0$`, and this player will win.

If they are not equal, then this player will still win. This player wins because she can choose the value of her move where either `1$1$` or `2$2$` is left as the final value.

Suppose `a=1$a=1$` and `b=2$b=2$`. If this player wants to have the final value as `1$1$`, then she will just choose `2$2$` and `1$1$` and replace them with `2−1=1$2-1=1$`. If she wants `2$2$`, then she will chose `1$1$` and `2$2$` and replace them with `1−2=−1$1-2=-1$`.

So, the player who makes the last move always wins. If `N$N$` is even, then Kitty wins, otherwise Katty wins.

Code

#include<bits/stdc++.h>

using namespace std;

int main()

{

 int t;

 cin>>t;

 while(t--)

 {

     int n;

     cin>>n;

     if(n==1)

     {

 

     cout<<"Kitty"<<endl;

     continue;

     }

 if(n%2==1)

     {

      cout<<"Katty"<<endl;

}

else cout<<"Kitty"<<endl;

 }

 return 0;

}