GNY07H - Tiling a Grid With Dominoes

#dynamic-programming #bitmasks

We wish to tile a grid 4 units high and N units long with rectangles (dominoes) 2 units by one unit (in either orientation). For example, the figure shows the five different ways that a grid 4 units high and 2 units wide may be tiled.

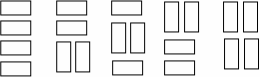
Write a program that takes as input the width, W, of the grid and outputs the number of different ways to tile a 4-by-Wgrid.

Input

The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the number of datasets that follow.

Each dataset contains a single decimal integer, the width, W, of the grid for this problem instance.

Output

For each problem instance, there is one line of output: The problem instance number as a decimal integer (start counting at one), a single space and the number of tilings of a 4-by-W grid. The values of W will be chosen so the count will fit in a 32-bit integer.

Explanation

Let T(n) be the number of ways one can tile a 3×n board with 2×1 tiles. Also, let P(n) be the number of ways one can tile a 3×n board with one corner removed with 2×1 tiles. Assumen sufficiently large (>= 4).

Then consider how you can start the tiling from the left (or right, doesn't matter).

You can place the tile covering the top left corner in two ways, vertical or horizontal. If you place it vertical, the tile covering the bottom left corner must be placed horizontally, giving a configuration

|
==

That leaves P(n-1) ways to tile the remaining part. If you place it horizontally, you can place the tile covering the bottom left corner either horizontally or vertically. If you place it vertically, you are in the same situation as before, just reflected, and if you place it horizontally, you must place a tile horizontally between them,

==
==
==

leaving you with a 3×(n-2) board to tile. Thus

T(n) = T(n-2) + 2*P(n-1)              (1)

Now, considering the 3×(n-1) board with one removed (already covered) corner (let's assume top left), you can either place a tile vertically below it, giving

=
|

and leaving you with a 3×(n-2) board to tile, or you can place two tiles horizontally below it, giving

=
==
==

and then you have no choice but to place another tile horizontally at the top, leaving you

===
==
==

with a 3×(n-3) board minus a corner,

P(n-1) = T(n-2) + P(n-3)

Adding up,

T(n) = T(n-2) + 2*(T(n-2) + P(n-3))
     = 3*T(n-2) + 2*P(n-3)                            (2)

But, using (1) with n-2 in place of n, we see that

T(n-2) = T(n-4) + 2*P(n-3)

or

2*P(n-3) = T(n-2) - T(n-4)

Inserting that into (2) yields the recurrence

T(n) = 4*T(n-2) - T(n-4)

q.e.d.

Solution

#include<bits/stdc++.h>

using namespace std;

int ha[30];

int hb[30];

#define ll long long int

ll dp[40];

int solve(int n)

{

if(n==0)

return 1;

if(n==1)

return 0;

if(n==3)

return 0;

if(n==2)

return 3;

if(n<0)

return 0;

 if(dp[n]!=-1)

 return dp[n];

 else

 {

   

 ll res=0;

 res+=4*solve(n-2)-solve(n-4);

 dp[n]=res;

 return res;}

}

int main()

{

     int n;

     memset(dp,-1,sizeof(dp));

     while(1)

 {

  cin>>n;

      if(n==-1)

  break;

  else 

  {

    ll res=solve(n);

    cout<<res<<endl;

}  

 }

 return 0;

}