D. Pair of Numbers

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Simon has an array a1, a2, ..., an, consisting of n positive integers. Today Simon asked you to find a pair of integers l, r (1 ≤ l ≤ r ≤ n), such that the following conditions hold:

1. there is integer j (l ≤ j ≤ r), such that all integers al, al + 1, ..., ar are divisible by aj;
2. value r - l takes the maximum value among all pairs for which condition 1 is true;

Help Simon, find the required pair of numbers (l, r). If there are multiple required pairs find all of them.

Input

The first line contains integer n (1 ≤ n ≤ 3·105).

The second line contains n space-separated integers a1, a2, ..., an (1 ≤ ai ≤ 106).

Output

Print two integers in the first line — the number of required pairs and the maximum value of r - l. On the following line print all l values from optimal pairs in increasing order.

Sample test(s)

input

5
4 6 9 3 6

output

1 3
2 

input

5
1 3 5 7 9

output

1 4
1 

input

5
2 3 5 7 11

output

5 0
1 2 3 4 5 

Note

In the first sample the pair of numbers is right, as numbers 6, 9, 3 are divisible by 3.

In the second sample all numbers are divisible by number 1.

In the third sample all numbers are prime, so conditions 1 and 2 are true only for pairs of numbers (1, 1), (2, 2), (3, 3), (4, 4), (5, 5).

A similar question to dominoes principle codeforces that uses the amortisation of o(n^2) dp to o(n).

Here we need just see an observation

           k......l........m

         

     if l divides any number before it suppose a[l] divides a[l-1] then it also divides all numbers that al divides.

   Hence we can go backwar in steps like these j-=dp[j]  and break when the jth element is not divisible by i.

      as further segment is not possible 

Now we do this in a forward fashion and backward fashion and generate the answer and the starting index.

Code

#include<bits/stdc++.h>

using namespace std;

struct node

{

  int f;

  int b;

} dp[300010];

int a[300010];

int main()

{

 int n;

 cin>>n;

 for(int i=1;i<=n;i++)

 {

   cin>>a[i];

 }

 for(int i=1;i<=n;i++)

 {

   dp[i].f=1;

   dp[i].b=1;

 }

 for(int i=1;i<=n;i++)

 {

 // cout<<"i "<<i<<endl;

   for(int j=i-1;j>=1;j-=dp[j].f)

   {

    //         cout<<" j  "<<j<<endl;

          if(a[j]%a[i]!=0)

          {

   //        cout<<"break for "<<j<<endl;

           break;

}

  //         cout<<"added  "<<j<<endl;

          dp[i].f+=dp[j].f;

 }

 }

 for(int i=n;i>=1;i--)

 {

    for(int j=i+1;j<=n;j+=dp[j].b)

     {

            if(a[j]%a[i]!=0)

break;

dp[i].b+=dp[j].b;  

}

 }

 /*for(int i=1;i<=n;i++)

 cout<<dp[i].f<<" ";

 cout<<endl;

 for(int i=1;i<=n;i++)

 cout<<dp[i].b<<" ";

 cout<<endl;*/

 

 int ans=0;

 int cnt=0;

 for(int i=1;i<=n;i++)

 {

          int temp=dp[i].f+(dp[i].b)-1;

          if(temp>=ans)

          {

           if(ans==temp)

           cnt++;

           else

           {

             cnt=1;

             ans=temp;

  }

  }

    

 }

 set<int> res;

 for(int i=1;i<=n;i++)

 {

        if(dp[i].f+(dp[i].b)-1==ans)

        {

// cout<<"i "<<i<<endl;

        res.insert(i-dp[i].f+1);

}

 }

 cout<<res.size()<<" "<<ans-1<<endl;

 int l=res.size();

 set<int>::iterator it;

 for(it=res.begin();it!=res.end();it++)

 {

   cout<<*it<<" ";

 }

 return 0;

}

E. Domino Principle

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Vasya is interested in arranging dominoes. He is fed up with common dominoes and he uses the dominoes of different heights. He put ndominoes on the table along one axis, going from left to right. Every domino stands perpendicular to that axis so that the axis passes through the center of its base. The i-th domino has the coordinate xi and the height hi. Now Vasya wants to learn for every domino, how many dominoes will fall if he pushes it to the right. Help him do that.

Consider that a domino falls if it is touched strictly above the base. In other words, the fall of the domino with the initial coordinate x and height h leads to the fall of all dominoes on the segment [x + 1, x + h - 1].

Input

The first line contains integer n (1 ≤ n ≤ 105) which is the number of dominoes. Then follow n lines containing two integers xi and hi( - 108 ≤ xi ≤ 108, 2 ≤ hi ≤ 108) each, which are the coordinate and height of every domino. No two dominoes stand on one point.

Output

Print n space-separated numbers zi — the number of dominoes that will fall if Vasya pushes the i-th domino to the right (including the domino itself).

Sample test(s)

input

4
16 5
20 5
10 10
18 2

output

3 1 4 1 

input

4
0 10
1 5
9 10
15 10

output

4 1 2 1 

First and the obvious aprroach is to sort the arrays int ascending/ descending order od starting indexes and 

then travese either backward or forward resepctively to get the answer.

Now the obvious soltion is an o(n^2) approach where for a decreasing start for any index we add the number of intemediate 

indexes + dp[j]

   i.e

         for(int i=1;i<=n;i++)

         {

             for(int j=i-1;j>=1;j--)

               {

                    if(dominoes j will fall when dominoe i is pushed)

                          dp[i]=max(dp[i],i-j+dp[j);

                }

          }

  Now this approach is 0(n^2) and will obviously fail, What we do is change the inner loop trickily

             i.e.  for(int j=i-1;j>=1;j-=dp[j])

                    {

                            //once we do this we substract go the index 

                            //  that doesnot fall due to 

                         // jth element , if the end of the ith dominoe

                       // is still covered by any dominoe we continue.

                          else

                             we break;

                     }

It may seem at first that the complexity of the jth loop is O(n) but we see that the inner loop travels a total of 

n times. summation(all traversals by j loop)=n;

                   

          This happens becuase suppose we have three element

 

                i  j.........k   l

  Now if the falling of i can cover j then we directly jump to l,and if it doesnot cover j then obviously it wont cover 

l.

Code

#include<bits/stdc++.h>

#define pb push_back

using namespace std;

struct node

{

 int s;

 int h;

 int dp;

 int id;

 }    a[100010];

bool comp(node a,node b)

{

 return a.s>b.s;

}

int ans[100010];

int main()

{

 int n;

 cin>>n;

 for(int i=1;i<=n;i++)

 {

   

   cin>>a[i].s>>a[i].h;

     a[i].id=i;

 }

 sort(a+1,a+1+n,comp);

 for(int i=1;i<=n;i++)

 a[i].dp=1;

 for(int i=1;i<=n;i++)

 {

   for(int j=i-1;j>=1;j-=a[j].dp)

   {

         if(a[j].s>a[i].s+(a[i].h)-1)

 break;

 a[i].dp+=a[j].dp;

 }

//  cout<<a[i].id<<" "<<a[i].dp<<endl;

 }

 

 for(int i=1;i<=n;i++)

 ans[a[i].id]=a[i].dp;

 for(int i=1;i<=n;i++)

 cout<<ans[i]<<" ";

 cout<<endl;

 return 0;

}

D. Babaei and Birthday Cake

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

As you know, every birthday party has a cake! This time, Babaei is going to prepare the very special birthday party's cake.

Simple cake is a cylinder of some radius and height. The volume of the simple cake is equal to the volume of corresponding cylinder. Babaei has n simple cakes and he is going to make a special cake placing some cylinders on each other.

However, there are some additional culinary restrictions. The cakes are numbered in such a way that the cake number i can be placed only on the table or on some cake number j where j < i. Moreover, in order to impress friends Babaei will put the cake i on top of the cake j only if the volume of the cake i is strictly greater than the volume of the cake j.

Babaei wants to prepare a birthday cake that has a maximum possible total volume. Help him find this value.

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 100 000) — the number of simple cakes Babaei has.

Each of the following n lines contains two integers ri and hi (1 ≤ ri, hi ≤ 10 000), giving the radius and height of the i-th cake.

Output

Print the maximum volume of the cake that Babaei can make. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .

Examples

input

2
100 30
40 10

output

942477.796077000

input

4
1 1
9 7
1 4
10 7

output

3983.539484752

Note

In first sample, the optimal way is to choose the cake number 1.

In second sample, the way to get the maximum volume is to use cakes with indices 1, 2 and 4.

Explanation

First of all, we calculate the volume of each cake: vi = π × hi × ri2.

Now consider the sequence v1, v2, v3, ..., vn : The answer to the problem is the maximum sum of elements between all increasing sub-sequences of this sequence. How do we solve this? First to get rid of the decimals we can define a new sequence a1, a2, a3, ..., ansuch that 

We consider dpi as the maximum sum between all the sequences which end with ai and

dpi = 

The answer to the problem is: π × maxi = 1ndp[i]

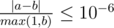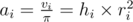
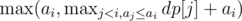
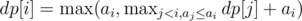Now how do we calculate  ? We use a max-segment tree which does these two operations: 1. Change the i't member to v. 2. Find the maximum value in the interval 1 to i.

Now we use this segment tree for the array dp and find the answer.

Consider that a1, a2, a3, ..., an is sorted. We define bi as the position of ai. Now to fill dpi we find the maximum in the interval [1, bi) in segment and we call it x and we set the bi th index of the segment as ai + x. The answer to the problem would the maximum in the segment in the interval [1,n]

Time complexity: O(nlgn)

Thanks to AlirezaT who helped a lot for writing the editorial of problem D.

Explanation

#include<bits/stdc++.h>

#include<stdio.h>

using namespace std;

#define ff first

#define ss second

#define mp make_pair

#define pb push_back

#define ll long long int

int male[400];

int female[400];

ll tree[600010];

bool cmp(pair<long long, int> a, pair<long long, int> b)

{

if (a.first != b.first)

return a.first < b.first;

return a.second>b.second;

}

ll query(int node,int s,int end ,int qs,int qh)

{

 if(qs>qh)

 return 0;

 if(s>end || qs>end || qh<s)

 return 0;

 if(s>=qs && end<=qh)

 return tree[node];

 int mid=(s+end)/2;

 ll q1=query(2*node,s,mid,qs,qh);

 ll q2=query(2*node+1,mid+1,end,qs,qh);

 return max(q1,q2);

}

void update(int node,int s,int end,int upl,int uph,ll val)

{

//cout<<"upl "<<" uph "<<upl<<" "<<uph<<endl;

  if(s>end || upl>end || uph<s)

  return ;

  if(s>=upl && end<=uph)

  {

      tree[node]=val;

      return ;

  }

  int mid=(s+end)/2;

  update(2*node,s,mid,upl,uph,val);

  update(2*node+1,mid+1,end,upl,uph,val);

  tree[node]=max(tree[2*node],tree[2*node+1]);

}

int main()

{

            int n;

            vector<pair<ll,int> > v;

            cin>>n;

            for(int i=0;i<n;i++)

            {

             ll a,b;

             cin>>a>>b;

             v.pb(mp(a*a*b,i));

}

sort(v.begin(),v.end(),cmp);

// cout<<"her e"<<endl;

for(int i=0;i<n;i++)

{

     int idx=v[i].ss;

//      cout<<"idc "<<idx<<endl;

         ll ans=query(1,0,n-1,0,idx-1);

//          cout<<"ans "<<ans<<endl;

         update(1,0,n-1,idx,idx,ans+v[i].ff);

//          for(int i=1;i<=11;i++)

//          cout<<"i "<<i<<tree[i]<<endl;

}

ll ans=query(1,0,n-1,0,n-1);

// cout<<ans<<endl;

double res=3.14159265*1.00*(double)ans;

printf("%.13lf",res);

return 0;

}