C. Amr and Chemistry

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Amr loves Chemistry, and specially doing experiments. He is preparing for a new interesting experiment.

Amr has n different types of chemicals. Each chemical i has an initial volume of ai liters. For this experiment, Amr has to mix all the chemicals together, but all the chemicals volumes must be equal first. So his task is to make all the chemicals volumes equal.

To do this, Amr can do two different kind of operations.

• Choose some chemical i and double its current volume so the new volume will be 2ai
• Choose some chemical i and divide its volume by two (integer division) so the new volume will be 

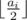
Suppose that each chemical is contained in a vessel of infinite volume. Now Amr wonders what is the minimum number of operations required to make all the chemicals volumes equal?

Input

The first line contains one number n (1 ≤ n ≤ 105), the number of chemicals.

The second line contains n space separated integers ai (1 ≤ ai ≤ 105), representing the initial volume of the i-th chemical in liters.

Output

Output one integer the minimum number of operations required to make all the chemicals volumes equal.

Sample test(s)

input

3
4 8 2

output

2

input

3
3 5 6

output

5

Note

In the first sample test, the optimal solution is to divide the second chemical volume by two, and multiply the third chemical volume by two to make all the volumes equal 4.

In the second sample test, the optimal solution is to divide the first chemical volume by two, and divide the second and the third chemical volumes by two twice to make all the volumes equal 1.

This is a very tricky question. Initially solving this question someone may be thoroughly misguided. But its a BFS implementation. First it is important to observe that, the maximum possible number that is supposed to be check is maximum in the array . As going beyond that wont yield anything. Because we can only multiply with 2. Now, the second part involves generating all the possible paths starting with arr[i] to maximum value and keeping a track of count and visited and hash function. If the hash of a particular value is n it means that all values can be vonstructed to that number. Hence we calculate the minimum of those indexes from 1 to maximum for which the hash value has the least number of steps.

** See the code for claritfications***

#include <iostream>

#include <cstdio>

#include <algorithm>

#include <cstring>

#include <string>

#include <cctype>

#include <stack>

#include <queue>

#include <vector>

#include <map>

#include <sstream>

#include <cmath>

#include <limits>

#include <utility>

#include <iomanip>

#include <set>

#include <numeric>

#include <cassert>

#include <ctime>

 

#define INF_MAX 2147483647

#define INF_MIN -2147483647

#define INF_LL 9223372036854775807LL

#define INF 2000000000

#define PI acos(-1.0)

#define EPS 1e-8

#define LL long long

#define mod 1000000007

#define pb push_back

#define mp make_pair

#define f first

#define s second

#define setzero(a) memset(a,0,sizeof(a))

#define setdp(a) memset(a,-1,sizeof(a))

#define bits(a) __builtin_popcount(a)

 

using namespace std;

 

int cnt[100005], vis[100005], steps[100005];

 

int main()

{

  //ios_base::sync_with_stdio(0);

  //freopen("lca.in", "r", stdin);

  //freopen("lca.out", "w", stdout);

  int n, res = INF, x, y;

  scanf("%d", &n);

  for(int i=1;i<=n;i++)

  {

    scanf("%d", &x);

    queue<pair<int, int> > q;

    q.push(mp(x, 0));

    while(!q.empty())

    {

      x = q.front().f;

      y = q.front().s;

      q.pop();

      if(x > 100003) continue;

      if(vis[x] == i) continue;

      vis[x] = i;

      steps[x]+=y;

      cnt[x]++;

      q.push(mp(x * 2, y + 1));

      q.push(mp(x / 2, y + 1));

    }

  }

  for(int i=0;i<=100000;i++)

    if(cnt[i] == n)

      if(res > steps[i])

        res = steps[i];

  printf("%d", res);

  return 0;

}