C. k-Tree

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Quite recently a creative student Lesha had a lecture on trees. After the lecture Lesha was inspired and came up with the tree of his own which he called a k-tree.

A k-tree is an infinite rooted tree where:

• each vertex has exactly k children;
• each edge has some weight;
• if we look at the edges that goes from some vertex to its children (exactly k edges), then their weights will equal 1, 2, 3, ..., k.

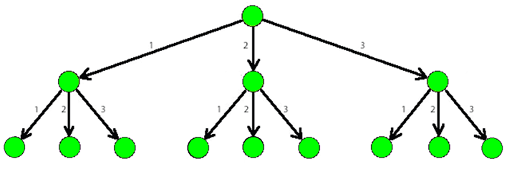
The picture below shows a part of a 3-tree.

As soon as Dima, a good friend of Lesha, found out about the tree, he immediately wondered: "How many paths of total weight n (the sum of all weights of the edges in the path) are there, starting from the root of a k-tree and also containing at least one edge of weight at least d?".

Help Dima find an answer to his question. As the number of ways can be rather large, print it modulo 1000000007 (109 + 7).

Input

A single line contains three space-separated integers: n, k and d (1 ≤ n, k ≤ 100; 1 ≤ d ≤ k).

Output

Print a single integer — the answer to the problem modulo 1000000007 (109 + 7).

Sample test(s)

input

3 3 2

output

3

input

3 3 3

output

1

input

4 3 2

output

6

input

4 5 2

output

7

Having read the statement properly the question reduces to finding the number of ways to write the permutation of numbers with maximum value being k(given) such that they add upto sum and using and edge of minimum value d.

The problem is solved recursively  using the state of dp as dp[sum][ison] signifying if the the value of sum is reached with using a value >=d or not.(ison=1 if a value more than d is used and is 0 if all values so far used are less than d).

   the return statements are

   if(sum<0)

return 0 (obviously there isnt any way)

 if(sum==0 && ison==1)

signifying that a number greater than d has been used than there is 1 way.

if(ison==0 && ison==0)

return 0 as the sum is reduced to 0 but no number has been used that is greater than d.

else we calculate dp[sum][ison]

         if the present edge value is less than d then we call solve(sum-i,ison|0) 

  why ison | 0??   suppose we have a state when we called (5,1)  then if d=2 then the value of ison for the next call if we fit the present edge as 1 should be 1 not 0 , because we have already used an edge that weighs greater than d.

     ***** the code follows here ****

#include<iostream>
#include<stdio.h>
using namespace std;
long long int dp[110][3];
#define mod 1000000007
int s,d ,k;
int solve(int sum, int ison)
{
        if(sum<0)
  return 0;
  if(sum==0 && ison==1)
  return 1;
  if(sum==0 && ison==0)
  {
   return 0;
  }
  if(dp[sum][ison]!=-1)
  {
   return dp[sum][ison];
  }
  else
  {
   dp[sum][ison]=0;
   for(int i=1;i<=k;i++)
   {
    if(i<d)
    dp[sum][ison]=(dp[sum][ison]+solve(sum-i,ison|0))%mod;
    else
    {
       dp[sum][ison]=(dp[sum][ison]+solve(sum-i,ison|1))%mod; 
    }
   }
  }
  return dp[sum][ison]; 
}
int main()
{
 for(int i=1;i<=103;i++)
 {
   dp[i][0]=-1;
   dp[i][1]=-1;
 }
 cin>>s>>k>>d;
 long long int  val=solve(s,0);
 cout<<val<<endl;
 return 0;
}

    ***** code ends here***