1017. Staircases Time limit: 1.0 second Memory limit: 64 MB One curious child has a set of N little bricks (5 ≤ N ≤ 500). From these bricks he builds different staircases. Staircase consists of steps of different sizes in a strictly descending order. It is not allowed for staircase to have steps equal sizes. Every staircase consists of at least two steps and each step contains at least one brick. 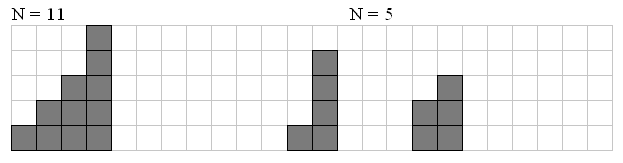Picture gives examples of staircase forN=11 and N=5: Your task is to write a program that reads the number N and writes the only number Q — amount of different staircases that can be built from exactly N bricks. Input Number N Output Number Q Sample input output 212 995645335

concept

This program involves dynamic programming as can be easily manifested .

Implemented using recursion . The state of the memoised arrar is dp[bricks used in previous state][brick remaining ] . We try to build the staircase with the remaining bricks. It is evident that if the remaining number of bricks is less than or equal to the number of bricks used in  previous state, then the possible ways is 0. If remaining ==0 the there is 1 way.(that is only n bricks in a single step).

The code is as follows 

#include<iostream>

#include<stdio.h>

using namespace std;

long long int dp[507][507];

long long int solve(int prev, int rem)

{

// cout<<"calling "<<prev<<" "<<rem<<endl;

if(rem==0)

return 1;

if(rem<=prev)

return 0;

if(dp[prev][rem]!=-1)

return dp[prev][rem];

long long int val=0;

for(int i=prev+1;i<=rem;i++)

{

val+=solve(i,rem-i);

}

dp[prev][rem]=val;

return dp[prev][rem];

}

int main()

{

for(int i=0;i<=502;i++)

{

for(int j=0;j<=502;j++)

dp[i][j]=-1;

}

int n;

cin>>n;

long long int val=0;

val=solve(0,n);

//cout<<dp[1][4]<<endl;

cout<<val-1<<endl;

}

/* code ends here */

We print val-1 as the position of the nth being lying in a single column needs to be subtracted as according to the question statement minimum number of steps is 2.